Desenvolvimento

Os métodos utilizados foram: 

1) mapa de concentração do teor de ''lead' na área mapeada em uma das margens do Rio Meuse;
2) mapa base;      

3) sumário da variável;      

4) histograma;      

5) box-plot;      

6) variograma experimental;      

7) variograma ajustado do obtido em 6);      

8) dispersograma das variáveis;       

9) cálculo do coeficiente de correlação;      

10) variação do teor de chumbo;      

11) mapa de isoteores (isopletas, contornos);      

12) mapa de contornos preenchidos.

Resultados:

1) Mapa de concentração do teor de ''lead' na área mapeada em uma das margens do Rio Meuse:
Foi necessário estimar os parâmetros de um modelo esférico omnidirecional de semivariograma que foram utilizados no programa de krigagem. Com as simulações, obteve-se:
Comando:

s.grid<-GridTopology(c( 178500, 329965),c(60,60),c(30,30))s.grid<-SpatialPoints(s.grid)gridded(s.grid)<-TRUEdata(meuse.all)v<-vgm(0.56439420,"Sph",535.8096,0.07655493)kr<-krige(lead~1,~x+y,model=v,data=meuse.all,newd=s.grid,nsim=3)spplot(kr["sim2"],xlab="Xloc(0-4)",ylab="Yloc(0-4)",main="Simulação Gaussiana 1")

x11()

Comando:

s.grid<-GridTopology(c( 178500, 329965),c(60,60),c(30,30))s.grid<-SpatialPoints(s.grid)gridded(s.grid)<-TRUEdata(meuse.all)v<-vgm(0.56439420,"Sph",535.8096,0.07655493)kr<-krige(lead~1,~x+y,model=v,data=meuse.all,newd=s.grid,nsim=3)spplot(kr["sim1"],xlab="Xloc(0-4)",ylab="Yloc(0-4)",main="Simulação Gaussiana 2")x11()

Mapa de concentração obtido baseado em krigagem simples:

Comando:

library(gstat)data(meuse.all)coordinates(meuse.all) = ~x+ydata(meuse.grid)gridded(meuse.grid) = ~x+y# grid já veio definidom <- vgm(.59, "Sph", 874, .04)x <- krige(log(lead)~1, meuse.all, meuse.grid, model = m,beta=5.9)l2 = list("SpatialPolygonsRescale", layout.north.arrow(), offset = c(181300,329800),scale = 400)spplot(x["var1.pred"], sp.layout=list(l2), col.regions=bpy.colors(20),key.space=list(x=0.1,y=.95,corner=c(0,1)), main = "simples kriging predictions", xlab="Xloc",ylab="Yloc ")

2) Mapa base:
Comando:

data(meuse.all)

plot(meuse.all[,2],meuse.all[,3],xlab='eixo x',ylab='eixo y',main='Mapa base dos pontos de coleta')

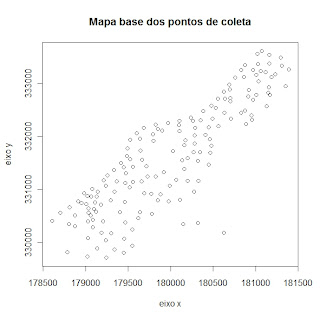
3) Sumário da variável:   

Comando:

library(gstat)    

data(meuse.all)   

attach(meuse.all) 

lead

pb=lead         

summary(pb)

Min. 1st Qu.  Median    Mean 3rd Qu.    Max.

  27.00   68.75  116.00  148.60  201.80  654.00

4) Histograma:  
Comando:

data(meuse.all)

g <- meuse.all

x.norm<- g$lead

h<-hist(x.norm,breaks=8)

xhist<-c(min(h$breaks),h$breaks)

yhist<-c(0,h$density,0)

xfit<-seq(0, 700, by=10)

yfit<-dnorm(xfit,mean=mean(x.norm),sd=sd(x.norm))

plot(xhist,yhist,type="s",ylim=c(0,max(yhist,yfit)),xlab="Pb",ylab="Frequência relativa",main="Histograma de Pb ")

lines(xfit,yfit,col="red")

   

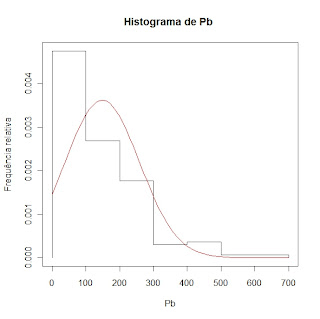
5) Box-plot: 
Comando: 

data(meuse.all)

vgm1<-variogram(log(lead)~1, locations=~x+y, data=meuse.all)

x=range(vgm1[,2])

y=range(vgm1[,3])

plot(x,y, asp = 1000, type = "n", main="Ajuste de um modelo teórico ao semivariograma")

points(vgm1[,2],vgm1[,3],col="blue",cex=1.5)

lines(vgm1[,2],vgm1[,3],col="blue")

f<-fit.variogram(vgm1,vgm(0.16, "Exp", 1500, 0.5))

v<-vgm(f$psill[2], "Exp",f$range[2],f$psill[1])

ff<-variogramLine(v,maxdist=1543 ,n = 15 , min = 80)

points(ff[,1],ff[,2],col = "red")

lines(ff[,1],ff[,2], col = "red")

asp=max(x)max(y)

asp=1542.27/0.6211689=2482.851 

6) Variograma experimental:
Comando:

data(meuse.all)

g=gstat(id='lead',formula=log(lead)~1,locations=~x+y,data=meuse.all)

grafico=variogram(g)

plot(grafico,main=' Variograma experimental de Pb',xlab='Distância',ylab='Semivariância') 

     

7) Variograma ajustado do obtido em 6):   
Comando:

data(meuse.all)

vgm1<-variogram(log(lead)~1, locations=~x+y, data=meuse.all)

x=range(vgm1[,2])

y=range(vgm1[,3])

plot(x,y, asp = 1000, type = "n", main="Ajuste de um modelo teórico ao variograma")

points(vgm1[,2],vgm1[,3],col="blue",cex=1.5)

lines(vgm1[,2],vgm1[,3],col="blue")

f<-fit.variogram(vgm1,vgm(0.16, "Exp", 1500, 0.5))

v<-vgm(f$psill[2], "Exp",f$range[2],f$psill[1])

ff<-variogram.line(v,maxdist=1543 ,n = 15 , min = 80)

points(ff[,1],ff[,2],col = "red")

lines(ff[,1],ff[,2], col = "red")

  model      psill    range

1   Nug 0.07655493   0.0000

2   Exp 0.56439420 535.8096


asp=max(x)max(y)
asp=1542.27/0.6211689=2482.851

Adotamos o valor 1000 por se tratar de ordem de grandeza

8) Dispersograma das variáveis:  

     

9) Cálculo do coeficiente de correlação: 

  

10) Variação do teor de chumbo:      
Com os mapas obtidos podemos observar que as concentrações do teor de chumbo estavam maiores quanto mais próximo ao leito do rio.

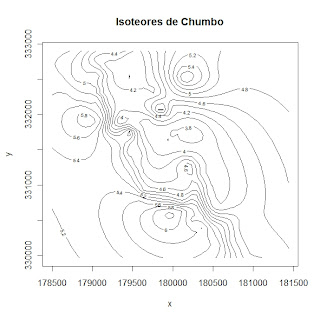
11) Mapa de isoteores:    
Comando:

s.grid<-GridTopology(c( 178500, 329965),c(60,60),c(50,50))

s.grid<-SpatialPoints(s.grid)

#spatial points

data(meuse.all)

m <- vgm(0.5643942, "Exp", 535.8096, 0.07655493)

xx <- krige(log(lead)~1, ~x+y, model = m, data = meuse.all, newd = s.grid)

dfxx<-as.data.frame(xx)                   

mz<-matrix(dfxx[,3], nrow=50, ncol=50, byrow=FALSE)

X11()

contour(x =seq(178500,181440,by= 60), y=seq(329965,332905,by=60),mz,nlevels=10,

xlab="x",ylab="y",main="isoteores de Chumbo")  

12) Mapa de contornos preenchidos:
Comando:
s.grid<-GridTopology(c(178500, 329965),c(60,60),c(50,50))
s.grid <- SpatialPoints(s.grid)
data(meuse.all)
m <- vgm(0.5643942, "Exp", 535.8096, 0.07655493)
xx <- krige(lead~1, ~x+y, model = m, data = meuse.all, newd = s.grid)
dfxx <- as.data.frame(xx)
mz <- matrix(dfxx[,3], nrow=50, ncol=50, byrow=FALSE)
nmz <- matrix(nrow=50, ncol=50)
for (i in 1:50)
for (j in 1:50)
{nmz[i,j]=mz[i,51-j]}
x =seq(1.0,5.9,by= 0.1)
y=seq(1,5.9,by=0.1)
filled.contour(x, y,nmz,nlevels=10,color=terrain.colors, xlab="X",ylab="Y",main="Mapa de Isoteores de Chumbo")